👉 View PDF
Chapter 10: WORK AND ENERGY
WORK
NOT MUCH
‘WORK’ IN SPITE OF WORKING HARD!
-
In science,
work is done only when a force causes displacement. Other activities do not
involve work. E.g.,
·
Studying,
reading, drawing and doing experiments expend energy, but little 'work' is
done.
·
Pushing a
rock without moving it involves no work.
·
Standing still with a load on the head involves no
work.
-
However,
climbing stairs or a tree involves work as there is displacement in the
direction of the applied force.
SCIENTIFIC
CONCEPTION OF WORK
-
When a force is exerted on an object and the object is displaced (moved),
work is done. E.g.,
·
Pushing a pebble or pulling a trolley causes movement.
·
Lifting a book requires force and the book moves.
·
A bullock
pulling a cart involves force & displacement.
-
It means, two conditions must be met for work:
·
A force should act on the object.
·
The object must be displaced.
WORK DONE BY A CONSTANT FORCE
-
Work is defined as the product of force and
displacement.
Work done = force × displacement
W = F s
W= the work done.
F= a constant force acting on an object.
s= displacement
of the object in the direction of force.
-
Work has
only magnitude and no direction.
-
If F
= 1 N and s = 1 m, the work done, W = 1 N m.
-
The unit
of work is newton metre (N m) or joule (J).
-
Thus 1 J
is the work done when a force of 1 N displaces an object by 1 m in the
direction of the force.
-
If the
force is zero, the work done is also zero. Similarly, if the displacement is
zero, no work is done.
Example: A force of 5 N is acting on an
object. The object is displaced through 2 m in the direction of the force. If
the force acts on the object all through the displacement, then work done is 5
N × 2 m =10 N m or 10 J.
Question: A force of 7 N acts on an
object. The displacement is, say 8 m, in the direction of the force. Let us
take it that the force acts on the object through the displacement. What is the
work done in this case?
Answer:
W = F s
Force
(F) = 7 N Displacement
(s) = 8 m
Work
done (W)= 7 N × 8 m = 56 Joules
-
When force
and displacement occur in same direction, the work done is the product of force
and displacement, and the work done is positive (e.g., a baby pulling a toy car
horizontally).
-
When a retarding force F is applied in the opposite direction of a
moving object, the angle between the force and displacement is 180°.
-
If the
object stops after a displacement s, the work done by the force is
negative. i.e., W= –F × s or F × (–s).
-
Thus, the work done by a force can be positive
or negative.
Activity
•
Lift an object up. The force exerted moves the object upwards, i.e., force
is in the direction of displacement. Force of gravity acts downward on the
object.
•
The work done by the lifting force is positive because it is in the
direction of displacement.
•
The work done by gravity is negative because it acts opposite to the
direction of displacement.
Example: A porter lifts a luggage of 15
kg from the ground and puts it on his head 1.5 m above the ground.
Calculate the work done by him on the luggage.
Solution:
Mass of luggage, m = 15 kg and displacement, s = 1.5
m.
Work done, W = F × s = mg × s
= 15 kg × 10 m s-2 × 1.5 m
= 225 kg m s-2 m
= 225 N m = 225 J.
ENERGY
-
All objects
acquire the capability of doing work through different means. E.g.,
·
A
fast-moving cricket ball hitting a stationary wicket causes the wicket to throw
away.
·
An object
raised to a height gains ability to do work.
·
A falling hammer drives a nail into wood.
·
A wound-up toy car moves when placed on the floor.
·
Pressing an air-filled balloon changes its shape.
If pressed gently, it returns to its original shape when the force is
withdrawn. If pressed hard, it explodes.
-
The capacity
of an object to do work is called energy.
-
The object
which does the work loses energy and the object on which the work is done gains
energy.
-
An object
can exert a force on another, transferring energy to the second object. So the
second object moves and does work.
-
Energy is
measured by its capacity to do work. So, the unit of energy is the same as that
of work, i.e., joule (J), named after James Prescott Joule.
-
1 J is the
energy required to do 1 joule of work.
-
1 kilo
joule (kJ) = 1000 J.
-
Various
forms energy: Mechanical energy (potential energy +
kinetic energy), heat energy, chemical energy, electrical energy and light
energy.
KINETIC
ENERGY
It is the energy possessed by an object due to its motion.
Activity
•
Drop a
heavy ball on a thick bed of wet sand from heights of 25 cm, 50 cm, 1 m, and
1.5 m. It creates depressions on the sand. The depth of the depression
increases with height, as a ball dropped from a greater height has more kinetic
energy. It exerts a stronger force on the sand and create a deeper dent.
Activity
•
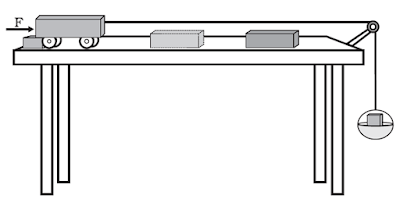
Set up the
apparatus as shown in figure.
•
Place a
wooden block of known mass in front of the trolley at a fixed distance.
•
Place a
known mass on the pan to start trolley moving.
•
The
trolley hits the wooden block, causing the block to be displaced. A stop should
be fixed on the table so the trolley stops after hitting the block.
•
The
displacement of the block indicates that work is done on it by the trolley, as
the block has gained energy.
•
This energy comes from the potential energy of the
mass on the pan, converted into kinetic energy of the
trolley.
•
Increasing
the mass on the pan increases the trolley's energy and results in greater
displacement of the block, meaning more work is done.
•
The moving trolley possesses energy as it performs
work.
-
A moving
object can do work. A faster object can do more work than a slower one. E.g., a
moving bullet can pierce a target, wind can turn the blades of a windmill.
-
Objects in
motion possess kinetic energy. E.g., A falling coconut, a speeding car, a
rotating wheel, a rolling stone, a flying aircraft, flowing water, a running
athlete etc. possess kinetic energy.
-
Kinetic energy
increases with the speed.
-
The kinetic
energy of a moving body is defined as the work done to accelerate it to its current
velocity.
-
The work done
on the object will cause a change in its velocity. Let its velocity change from
u to v.
v2 – u2 = 2a s
F = m a
The work done, W = F s.
-
If the
object is starting from its stationary position, i.e., u = 0, then
W = ½ m v2
The
work done is equal to the change in the kinetic energy of an object. Thus, the
kinetic energy (Ek) of an object with mass, m
moving with a uniform velocity, v is
Ek = ½ m v2
Example: An object of mass 15 kg is moving
with a uniform velocity of 4 m s–1. What is the kinetic energy possessed
by the object?
Solution:
Mass, m = 15 kg,
velocity, v = 4 m s–1.
Kinetic energy, Ek
= ½ m v2
½ × 15 kg × 4 m s–1 × 4
m s–1 = 120 J.
Example: What is the work to be done to
increase the velocity of a car from 30 km h–1 to 60 km h–1
if the mass of the car is 1500 kg?
Solution:
Mass of the car, m
=1500 kg
The final velocity of
the car, v = 60 km h–1 = 50/3 m s–1.
؞ the initial kinetic
energy of the car, Eki = ½ m u2
= ½ × 1500 kg × (25/3 m
s–1)2 = 156250/3 J.
The final kinetic energy
of the car,
Ekf = ½ × 1500 kg × (50/3 m s–1)2 = 625000/3 J.
The work done = Change
in kinetic energy
= Ekf –
Eki = 156250 J.
POTENTIAL
ENERGY
It is the stored energy of an object due to its position or configuration.
Activity 1
•
When a
rubber band is stretched, it acquires potential energy. This energy comes from
the work done on the band by pulling it. When released, the stored energy is
converted back into kinetic energy as the band returns to its original length.
Activity 2
•
Take a slinky and stretch it by holding one end while moving away from
the other end.
•
Release the slinky. It returns to its original shape.
•
Energy is stored as potential energy when stretched.
•
Energy is also stored when compressed, acting as potential energy.
Activity 3
•
Place a wound-up
toy car on the ground. It moves.
•
It
acquires energy from the potential energy stored in the wound-up spring.
•
The energy acquired depend on the number of
windings. More windings store more potential energy.
•
It can be
tested by winding the car different numbers of times and measuring the distance
it travels each time.
Activity 4
•
Lift an
object to a certain height. It can now do work.
•
It begins
to fall when released. This implies that it has acquired some energy.
•
If raised
to a greater height it can do more work and hence possesses more energy. This energy
is acquired from the work done against gravity during lifting.
-
Energy transferred to an object is stored as potential energy if not
used to change its velocity.
-
When a person stretches a rubber band, his energy is transferred to it,
which becomes its potential energy.
-
Winding a toy car's key involves work, storing energy in the spring as
potential energy.
Activity
•
Make a
bamboo bow, place a light stick arrow on it, stretch the string, and release
the arrow.
• The arrow flies off as the shape of the bow changes. The potential energy stored in the bow due to the change of shape is used as kinetic energy to throw off the arrow.
POTENTIAL
ENERGY OF AN OBJECT AT A HEIGHT
-
When
an object is raised, work is done against gravity. So, its energy (gravitational
potential energy) increases.
-
Gravitational
potential energy is the work done to raise an
object from the ground to a point against gravity.
-
Consider
an object of mass, m is raised through a height, h from the
ground.
-
The
minimum force required to raise the object is equal to object’s weight, mg and the
work done on the object against gravity is W.
i.e., work done, W = force × displacement
= mg × h =
mgh
-
This work equals potential energy (EP)
gained by the object.
i.e., Ep = mgh
Potential energy of an object at a height varies depending on the chosen
reference point (ground level or zero level). The same object can have
different potential energy values based on the level used for measurement.
-
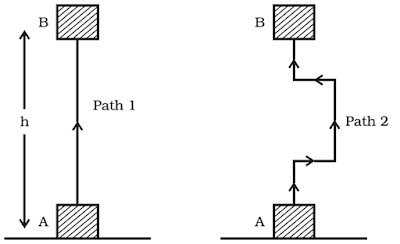
The work
done by gravity depends on the difference in vertical heights between the
initial and final positions of the object, not the path taken. Consider a block
is raised from position A to B via two different paths. In both cases, height
AB = h, and the work done is mgh.
Example: Find the energy possessed by an
object of mass 10 kg when it is at a height of 6 m above the ground. Given, g
= 9.8 m s–2.
Solution:
Mass of the object, m = 10 kg
Displacement (height), h = 6 m
Acceleration due to gravity, g = 9.8 m s–2.
Potential energy = mgh
= 10 kg × 9.8 m s–2 × 6 m = 588 J.
Example: An object of mass 12 kg is at a
certain height above the ground. If the potential energy of the object is 480
J, find the height at which the object is with respect to the ground. Given, g
= 10 m s–2.
Solution:
Mass of the object, m = 12 kg
Potential energy, Ep = 480 J.
Ep = mgh
480 J = 12 kg × 10 m s–2 × h
ARE
VARIOUS ENERGY FORMS INTERCONVERTIBLE?
Energy can be converted from one form to
another.
Examples from Nature:
·
Green Plants: During
photosynthesis, solar energy is converted into chemical energy.
·
Air Movement: Solar energy heats the Earth's surface, causing wind, converting solar energy into kinetic energy.
·
Fuels: Coal & petroleum store chemical energy formed from ancient
organic matter over time.
·
Water Cycle: Solar
energy drives evaporation, condensation, and precipitation, sustaining the
cycle.
Human Activities & Gadgets:
·
Electric Bulb: Converts
electrical energy to light & heat.
·
Car Engine: Converts
chemical energy (fuel) to mechanical energy.
·
Wind Turbine: Converts
kinetic energy (wind) to electrical energy.
LAW OF CONSERVATION OF ENERGY
-
It states
that, energy can only be converted from one form to another; it can neither be
created or destroyed. The total energy before and after the transformation
remains the same.
-
This law
is valid in all situations and for all kinds of transformations.
-
E.g., Let
an object of mass, m is falling freely from a height, h. At the
start, potential energy is mgh and kinetic energy is zero because its
velocity is zero. Thus, total energy of the object is mgh.
- As the object falls, potential energy decreases
while kinetic energy increases. When it approaches the ground, height, h=0
and velocity, v will be the highest. Therefore, kinetic energy is
greatest and potential energy is least. However, the total energy remains
constant throughout the fall.
i.e., potential energy + kinetic energy = constant
or mgh + ½ mv2 = constant.
-
Sum of kinetic
energy and potential energy of an object is its total mechanical
energy.
-
During
free fall, the decrease in potential energy at any point equals the increase in
kinetic energy (here, effect of air resistance is ignored). Thus, there is a
continual transformation of gravitational potential energy into kinetic energy.
Activity: An object of mass 20 kg is dropped from a height of 4 m. Fill in the
blanks in the following table by computing the potential energy and kinetic energy.
g = 10 m s–2.
Answer:
|
Height at which object is located
m |
Potential energy (Ep= mgh) J |
Kinetic energy (Ek= mv2/2) J |
Ep + Ek
J |
|
4 |
800 |
0 |
800 |
|
3 |
600 |
200 |
800 |
|
2 |
400 |
400 |
800 |
|
1 |
200 |
600 |
800 |
|
Just above ground |
0 |
800 |
800 |
-
If nature had no transformation of energy, life would not exist, as all
organisms depend on energy conversions to sustain biological processes. E.g., plants
convert solar energy into chemical energy through photosynthesis.
RATE
OF DOING WORK
Activity
•
Two
children, A and B, of equal weight climb an 8-meter rope. A takes 15 seconds,
while B takes 20 seconds to finish the task. Though both do the same work by
reaching the same height, A finishes faster. It indicates A has a higher rate
of work or power.
-
A stronger
person does work faster. A more powerful vehicle completes a journey in a
shorter time.
-
Machines
like motorbikes and cars are classified based on how quickly they change energy
or do work.
-
Power
measures the speed of work done. It is defined as the rate of doing work or the
rate of transfer of energy.
-
If an agent
does a work W in time t, then
Power = work/time or P = W/t
-
Unit of
power is watt (W) [in honour of James Watt].
-
1 watt is the power of an agent working at the rate of 1 joule per second.
-
Power is 1
W when the rate of consumption of energy is 1 J s–1. i.e., 1 watt (W)
= 1 joule/second (1 J s–1).
- Larger energy
transfer rate is measured in kilowatts (kW).
-
1 kilowatt
(kW)= 1000 watts (W) or 1000 J s–1.
-
Power of
an agent may vary with time. This means that work may be done at different
rates at different intervals of time. So, Average power is calculated by
dividing total energy consumed by the total time taken.
Example: Two girls A and B, each of weight 400 N climb up a rope through a
height of 8 m. A takes 20 s while B takes 50 s to accomplish this task. What is
the power expended by each girl?
Solution:
(i)
Power
expended by girl A:
Weight of the girl, mg = 400 N
Displacement (height), h = 8 m
Time taken, t = 20 s
Power, P = Work done/time taken
(ii) Power expended by girl B:
Weight of the girl, mg = 400 N
Displacement (height), h = 8 m
Time taken, t = 50 s
Example: A boy of mass 50 kg runs up a
staircase of 45 steps in 9 s. If the height of each step is 15 cm, find his power.
Take g = 10 m s–2.
Solution:
Weight of the boy, mg
= 50 kg × 10 m s–2 = 500 N
Height of the staircase,
h = 45 × 15/100 m = 6.75 m
Time taken to climb, t
= 9 s
👉 View PDF